Example of Engineering Problem Solving Strategy

Problem Statement:

A ball is through into the air with a velocity of 1.0 m/sec. at a 45 ° angle. Calculate the time it takes before it hits the ground. Assume that the ball is initially 1m above the ground.
(This is actually a problem from Physics, but quite similar to engineering problems)

Step1. Problem Abstraction

First draw a figure depicting the scenario outlined in the problem.

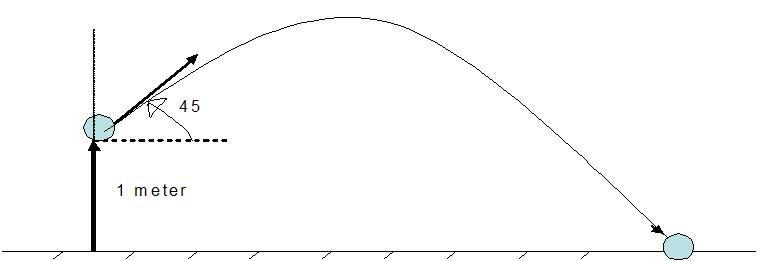
.Needed: time to hit the ground
Given: Initial velocity and direction and initial location.
Abstraction: Ball goes up and is pulled down by gravity and follows a “parabolic” path ( from empirical observation of thrown objects). Vertical velocity will decrease, become zero and then become negative. Motion in vertical and horizontal directions can be decoupled.

Step 2. List of Variables

We will need vertical and horizontal velocities, v x and v y
Initial Velocities are known:
v xo = (1m/sec) cos 45 °= 0.707 m/s
v yo = (1m/sec) sin 45° = 0.707 m/s
d y = vertical distance traveled by the ball, m
t = time, sec

Step 3. Basis for Calculation

None required for this problem

Step 4. Assumptions

1. Ground is flat
2. Air resistance can be neglected
3. Acceleration due to gravity is 9.8 m/sec 2

Step 5. List References

Physics Text, p.135

Step 6. Develop model Equations

The vertical motion is governed by the equation (from the definition of acceleration). We define a new variable, y (meters) to indicate the vertical distance from the ground. The variable g is used to indicate the acceleration due to gravity (assumed constant, another assumption).

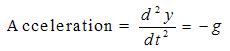
Initial position (t=0) y = 1.0 m; Initial vertical velocity = 0.707 m/s

Step 7. Solve

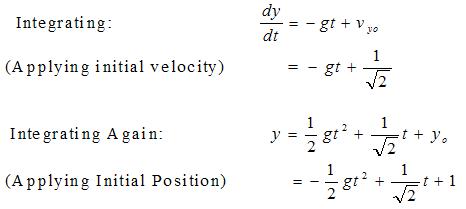
We want to know when the ball hits the ground (y = 0).

Substituting for

we obtain: t = 0.529 sec or t = -0.385 sec
Negative answer is not acceptable. Hence time to hit the ground = + 0.529 sec.

Step 8. Interpret Solution

The answer seems reasonable from an intuitive point of view. The ball does not travel far before it hits the ground. You can get a physical feel for the answer by throwing the ball yourself and seeing how long it takes to hit the ground.